「使数　p49の３」

（テーマ提供者　甲斐町さん）

　掲示板の記録メニューへ　　トップページへ

お願い  投稿者：甲斐町  投稿日：11月17日(金)17時54分39秒 　 引用
  使いこなす数学2年の49ページ3番の問題が文章が長すぎる上に正方形の中に点が二つあるので絵のイメージさえ掴めません。
答えの解説を読んでも分からないので、解説をお願いします。

佑さんも数学でめちゃめちゃ悩んでるみたいです。 		 
Re: お願い  投稿者：ガジ  投稿日：11月17日(金)21時48分38秒 　 引用
  > 答えの解説を読んでも分からないので、解説をお願いします。
日曜日にはＵｐします。
少し待っていてください。
　図のように、１辺の長さ６cmの正方形ABCDがあります。
　点Pは辺AD上を動き、頂点Aをスタートし、頂点Dまで行って頂点Aに戻ります。
　点Qは辺BC上を動き、点Pと同時に頂点Bをスタートし、頂点Cまで動きます。
　点Pの速さを毎秒２cm、点Qの速さを毎秒１cmとするとき、
スタートしてからx秒後の四角形PBQDの面積をy平方cmとします。
　このとき、x,yの関係をグラフに表しなさい。
　　（ただし、点Pが点Aにあるときは△PBD
　　　　　　　　点Pが点Dと一致するときは△PBQ
　　　　　　　　　　　　　　　　　　　　　　・・・の面積をy平方cmとします。）

確かに、　　y=-3x+18　(0≦x≦3)
　　　　　　　y=　9x-18　(3≦x≦6)　　　　なんだけれど

　　まずは、１秒後、２秒後・・・・と具体的に考えてみる方がいい。
　　図を書いてみれば、下の通り。
　　具体的な数値で点を打っていけばグラフが書けてしまいます。
x秒後 その時の様子 左上の三角形
△APB
底辺　AP 　
高 さ　PB=6		 右下の三角形
△DBC
底辺　ＱＣ　
高 さ　ＣＤ=6		 　y
=36-△APB-△DBC
x=0 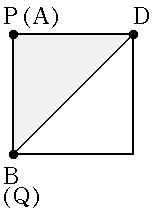AP=0
BP=6


　　△APB
　=0×6÷2
　=0		 QC=6
CD=6


　　△DBC
　=6×6÷2
　=18		 　 36-0-18
＝18
x=1 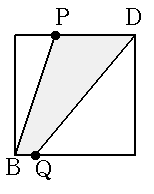AP=2
BP=6


　　△APB
　=2×6÷2
　=6		 QC=5
CD=6


　　△DBC
　=5×6÷2
　=15		 　 36-6-15
＝15
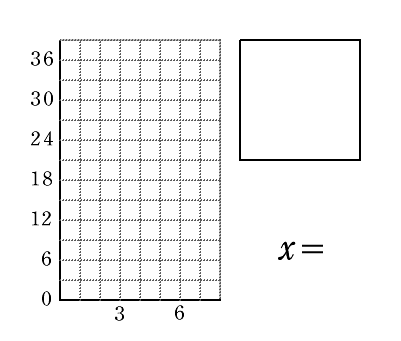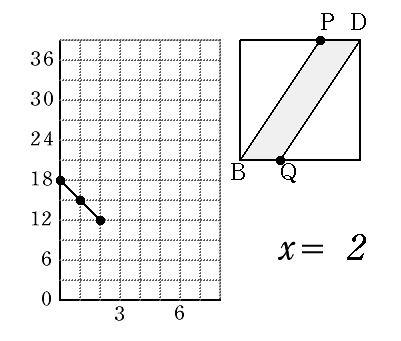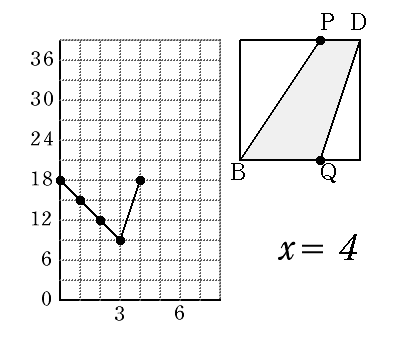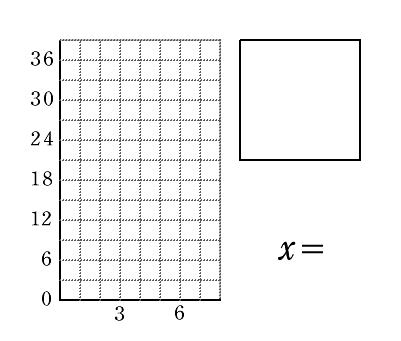
x=2 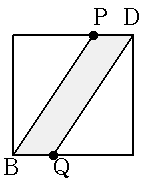AP=4
BP=6


　　△APB
　=4×6÷2
　=12		 QC=4
CD=6


　　△DBC
　=4×6÷2
　=12		 　 36-12-12
＝12
x=3 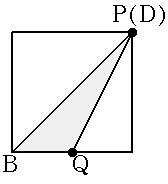AP=6
BP=6


　　△APB
　=6×6÷2
　=18		 QC=3
CD=6


　　△DBC
　=3×6÷2
　= 9		 　 36-18-9
＝9
x=4 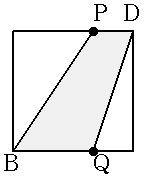AP=4
BP=6


　　△APB
　=4×6÷2
　=12		 QC=2
CD=6


　　△DBC
　=2×6÷2
　=6		 　 36-12-6
＝18
x=5 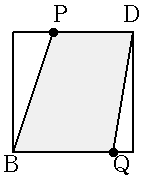AP=2
BP=6


　　△APB
　=2×6÷2
　=6		 QC=1
CD=6


　　△DBC
　=1×6÷2
　=3		 　 36-6-3
＝27
x=6 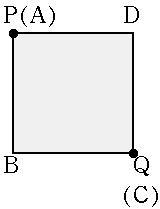AP=0
BP=6


　　△APB
　=0×6÷2		 QC=0
CD=6


　　△DBC
　=0×6÷2		 　 36-0-0
＝36