俀侽侾俀丏俈丏俀俋
暘偐傝傗偡偄旝暘丒愊暘偵偮偄偰
丂丂丂丂
塱堜寶嵠
丂嶲峫乯儕儞僋愭丂慺悢暘晍偺尋媶
旝暘丒愊暘偲暦偔偩偗偱嬯庤堄幆偺傾儗儖僊乕偺恖傕偄傞偩傠偆偟丄偁傞偄偼偦傟埲慜偵暦偒側傟側偄尵梩偩偲巚偆恖偑偄傞偐傕偟傟側偄丅妋偐偵擔忢偺夛榖偱偼側偐側偐弌偰偙側偄悢妛忋偺岅渂偱偁傞丅偟偐偟尰徾偲偟偰偼擔忢偺惗妶偵偄偔傜偱傕懚嵼偟偰偍傝丄壢妛偺媶柧偵偍偄偰傕嬌傔偰戝帠側婎杮揑側悢妛偱偁傞丅偟偨偑偭偰悢妛傗壢妛偺愱栧偱側偄堦斒偺恖偱傕丄旝暘丒愊暘偲偼丄偍傛偦偳傫側偙偲偱丄壗屘昁梫側偺偐傪抦傞偙偲偼戝帠偩偲巚偆丅丂偦偙偱嬶懱揑側椺偱棟夝傪怺傔偰傕傜偄丄悢妛偲偺壦偗嫶偲側傞傛偆偵丄暘偐傝傗偡偔愢柧傪偡傞丅
嘥旝暘丒愊暘偺奣擮乮悢幃傪梡偄偢愢柧乯
侾丂旝暘偺奣擮
丂旝暘偡傞偲偼娙扨偵偄偊偽曄壔偡傞検偺妱崌傪媮傔傞偙偲傪偄偆丅椺偊偽幵偱憱峴偡傞偲偳傫偳傫憱峴嫍棧偑憹偊丄堦帪娫偁偨傝偳傟偩偗憱偭偨偐偼帪懍壗俲倣偲偄偆懍搙偱昞偝傟傞丅偙偺扨埵帪娫偁偨傝偺嫍棧偺曄壔丄偡側傢偪懍搙偑旝暘抣偲偟偰昞偝傟傞丅偙偺傎偐曄壔偡傞傕偺偼擔忢惗妶偵堦攖偁傞丅椺偊偽巕嫙偺恎挿傗塉検側偳帪娫揑偵曄壔偡傞傕偺丄帪娫揑側曄壔偱側偔偰傕丄廂擖偺憹尭偵敽偆擺惻妟傗丄懱廳偺曄壔偵敽偆暊埻偺曄壔側偳怓乆偁傞丅偙傟傜偼偡傋偰偦傟偧傟偺帪揰偱偺曄壔棪偑懚嵼偡傞丅
偱偼壗屘偦偺曄壔棪傪傢偞傢偞旝暘側偳擄偟偄尵偄曽傪偡傞偺偐偲偄偆媈栤偑桸偄偰偔傞丅偦傟偼偙傟偐傜弴師愢柧偟偰偄偔偑旝暘偲偼悢妛揑側庤抜偱偁傝寁嶼偵傛偭偰偦偺曄壔棪傪媮傔傞偙偲偑偱偒傞偐傜偱偁傞丅堦掕偺曄壔棪乮椺偊偽堦掕懍搙乯側傜娙扨偩偑丄曄壔棪帺懱偑曄壔偟偰偄傞乮椺偊偽帪娫偵傛偭偰懍搙偑堎側傞乯応崌偼偙偺寁嶼庤抜偑昁梫偲側偭偰偔傞丅
偱偼師偵幵偺懍搙偺椺偱旝暘傪愢柧偡傞丅

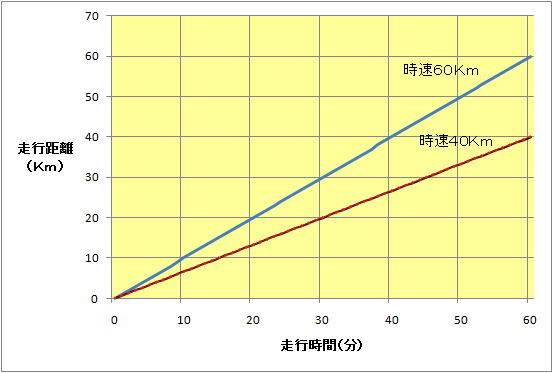
恾侾丂堦掕懍搙偵偍偗傞憱峴帪娫偲嫍棧偺娭學
恾侾偼堦掕懍搙偱偺帪娫偲嫍棧偺娭學傪帵偟偰偄傞丅惵慄偼帪懍俇侽俲倣偺応崌偱偁傞丅堦掕懍搙偱偁傞偐傜侾帪娫屻偵俇侽俲倣憱傝丄侽丏俆帪娫側傜偦偺敿暘偺俁侽俲倣偲捈慄娭學偵側傞丅帪懍係侽俲倣偺応崌乮愒慄乯傕摨條偵侾帪娫屻偵係侽俲倣偱丄帪娫偵斾椺偟偨捈慄娭學偵側傞.丅偙偺懍搙偺嵎偼僌儔僼偺忋偱偳偆堘偆偐偲偄偆偲丄捈慄偺孹偒乮岡攝乯偑堘偆偙偲偑梕堈偵暘偐傞丅懍搙偺懍偄曽偑孹偒偼棫偭偰偍傝丄抶偄曽偑怮偰偄傞丅偙偺岡攝偺嵎偑懍搙嵎偱偁傞丅偙傟偼師偺堦掕懍搙偱側偄応崌偺愢柧偱廳梫側栶妱偲側傞
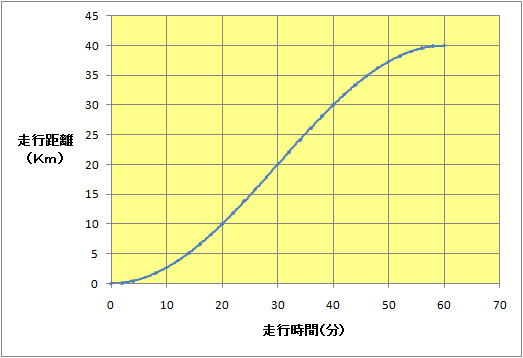
恾俀丂懍搙堦掕偱側偄応崌偺憱峴帪娫偲嫍棧偺娭學
恾俀偼帪娫偲嫍棧偺娭學偑捈慄偱側偄応崌丄偮傑傝堦掕懍搙偱側偄応崌偺椺偱偁傞丅嵟弶偺侽丏侾帪娫偼侾乣俀俲倣偟偐恑傫偱偄側偄偺偵搑拞偺侽丏俆乣侽丏俇帪娫偺娫偼俆倠倣埲忋恑傫偱偍傝懍搙偑懍偄偺偑暘偐傞丅丂慡懱偲偟偰偼侾帪娫屻偵係侽俲倣憱峴偟偨偐傜暯嬒懍搙偼帪懍係侽俲倣偱偁傞偙偲偼妋偐偱偁傞偑丄拞娫偺侽.俆帪娫偱偺懍搙偼偳偆偩傠偆丠偳偆偟偰媮傔傟偽椙偄偺偩傠偆丅
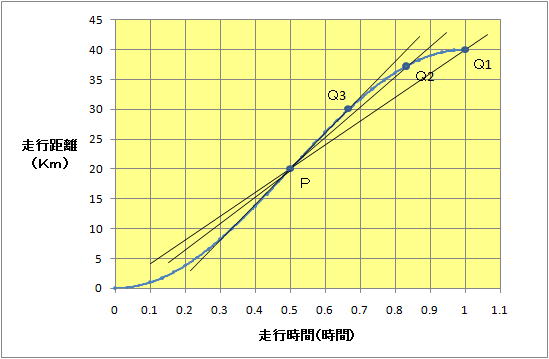
恾俁丂俹揰偱偺懍搙偺媮傔曽
恾俁偼恾俀偲摨偠憱峴帪娫偲嫍棧偺娭學偺僌儔僼偱偁傞偑丄拞娫揰偱偁傞侽丏俆帪娫偱偺懍搙偺媮傔曽傪恾帵偟偰偄傞丅傑偢嵟弶丄恾偵偁傞俹偲俻侾娫偺暯嬒懍搙傪媮傔傞丅偙傟偼俹偲俻1傪寢傫偩捈慄偱偁傝丄敿帪娫偱俀侽俲倣恑傫偱偄傞偺偱偙偺娫偺暯嬒帪懍偼係侽俲倣偱偁傞丅偮傑傝帪懍係侽俲倣偺岡攝偲偄偊傞丅偟偐偟偙偺懍搙偼俹揰偺懍搙偲偼尵偊側偄偺偱丄師偵傛傝俹揰偵嬤偄俹揰偲俻2揰娫偺暯嬒懍搙傪尒偰傒傛偆丅偙傟偼摨條偵俹揰偲俻2揰傪寢傇捈慄偱偁傞丅愭傎偳傛傝岡攝偑棫偭偰偍傝暯嬒懍搙偑懍偄丅偝傜偵俻3揰傪寢傇捈慄偱偺懍搙偲丄偳傫偳傫嬋慄忋偱俹揰偵嬤偯偗偽俹揰偺懍搙偵嬤偯偔丅偦偟偰岡攝偼俹揰偵嬤偯偔偵偮傟丄曄壔偼彮側偔側傝堦掕偺岡攝偵嬤偯偔丅姰慡偵俹揰偲廳側傞偲揰偵側傝捈慄偱側偔側傞偑丄尷傝側偔俹揰偵嬤偯偗偨帪偺捈慄傪俹揰偵偍偗傞愙慄偲屇傇丅偦偟偰偙偺愙愴偺岡攝偙偦偑丄偦偺揰偵偍偗傞懍搙傪昞偡丅丂
旝暘傕偙偺嶌恾偲慡偔摨偠峫偊曽偱峴偆丅俹偲俻偺俀揰娫偺嫍棧傪尷傝側偔旝彫偵偟偨曄壔棪傪媮傔傞偲偄偆堄枴偱旝暘偲偄偆尵梩偑巊傢傟偰偄傞丅偨偩悢妛偲偟偰旝暘偡傞偵偼丄帪娫偲嫍棧偺娭學偑旝暘壜擻側悢幃偱昞偣偰偄側偄偲旝暘偱偒側偄丅偄偐偵悢妛偲偄偊偳丄庤彂偒偱帺桼偵嬋慄傪昤偄偰偙傟傪旝暘偣傛偲偄傢傟偰傕偱偒側偄偺偱偁傞乮偦偺嬋慄偵嬤偄幃偵抲偒姺偊偰旝暘偡傞偲偄偭偨嬤帡朄偟偐側偄乯丅嬋慄偺幃偑梌偊傜傟偽丄偦傟傪旝暘偟偨幃偼嬋慄偺奺揰偺愙慄傪昞偡幃偲側傞丅恾俁偼嶰妏娭悢偺娭學幃偱偁傞乮幃偼徣棯乯偑丄偙傟傪旝暘偟偰帪娫偲懍搙乮愙愴偺岡攝乯偺娭學幃偑摼傜傟傞丅偦偺寢壥偼恾係偺捠傝丅丂
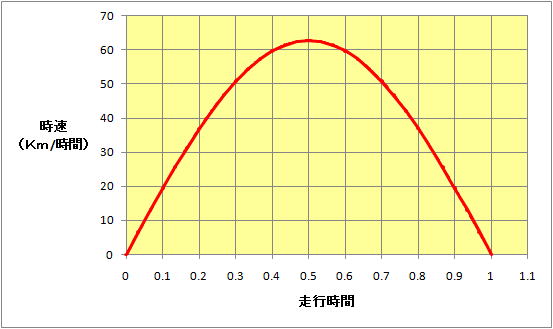
恾係丂憱峴帪娫偲懍搙乮旝暘寢壥乯
弌偩偟僛儘偐傜偩傫偩傫壛懍偟偰侽丏俆帪娫屻偵偼嵟崅懍搙丄栺俇俁俲倣/帪娫偵払偟偦傟偐傜偳傫偳傫尭懍偟偰侾帪娫偺偪偵偼掆巭偡傞偲偄偆娭學偑摼傜傟偨丅奺帪娫偱偺愙慄傪偄偪偄偪嶌恾偟偰媮傔側偔偰傕丄懳徾偺侾帪娫埲撪偺偳偺帪揰偺懍搙傕媮傔傜傟偨丅偙傟偑旝暘偲偄偆悢妛偺晲婍偵傛傞埿椡偱偁傞丅悢幃傪旝暘偡傞偺偼彮偟擄偟偔側傞偺偱嫽枴偺偁傞恖偼師崁偺旝暘偺婎慴寁嶼傪嶲徠丅
俀丂愊暘偺奣擮
愊暘偲偼娙扨偵偄偊偽旝暘偲媡偺憖嶌偱偁傞丅愭偺椺偱偄偊偽丄憱峴帪娫偲嫍棧偺娭學乮恾俀乯傪旝暘偟偰憱峴帪娫偲懍搙偺娭學乮恾係乯傪摼偨偑丄媡偵憱峴帪娫偲懍搙偺娭學乮恾係乯傪愊暘偟偰憱峴帪娫偲嫍棧偺娭學乮恾俀乯偑摼傜傟傞丅丂傑偢娙扨側椺偐傜峫偊傛偆丅丂壓恾俆偼懍搙堦掕偱侾帪娫憱峴偟偨応崌偱偁傞丅
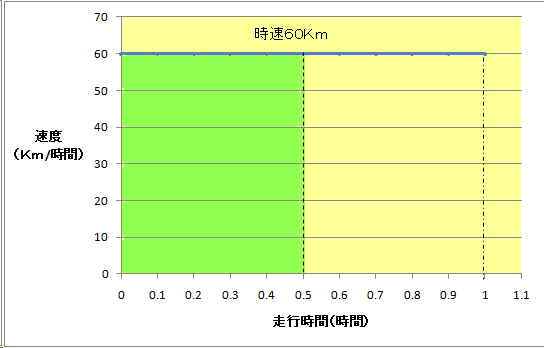
恾俆丂懍搙堦掕偺応崌
惵怓偺慄偼丄堦掕懍搙60俲倣/帪娫傪昞偟偰偄傞丅偳偺帪娫傪庢偭偰傕60俲倣/帪娫側偺偱墶堦捈慄偵側偭偰偄傞丅偝偰偙偺帪憱峴嫍棧傪峫偊偰傒傛偆丅侾帪娫屻偼摉慠偺偙偲側偑傜60俲倣傪憱偭偨偙偲偵側傞丅偱偼0.5帪娫乮敿帪娫乯偱偼偳偆偩傠偆丅偙傟偼60俲倣/帪娫亊0.5帪娫偩偐傜30俲倣偱偁傞偙偲偑傢偐傞丅偙傟傪忋偺僌儔僼偺恾偱傒傞偲憪怓偺柺愊偵憡摉偡傞丅
懠偺帪娫偱傕帪娫偲懍搙偺愊偱偁傞偐傜丄偦傟偱宍惉偝傟傞挿曽宍偺柺愊傪媮傔傟偽傛偄偙偲偑暘偐傞丅偙偺柺愊傪媮傔傞偙偲偑愊暘側偺偱偁傞丅帪娫偑宱偮偵廬偭偰柺愊偑憹偊偰愊嶼偝傟偰偄偔偙偲偑暘偐傞丅偦偙偐傜愊暘偲偄偆尵梩偑偱偒偨丅師偵懍搙堦掕偱側偄応崌傪傒偰傒傞丅
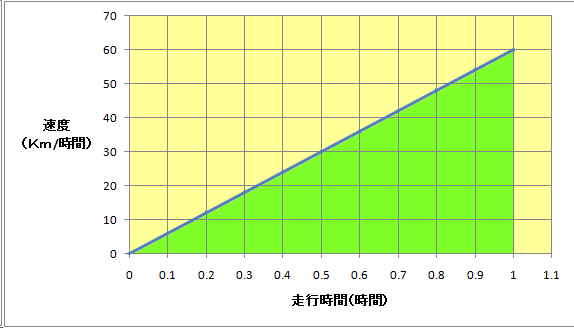
恾俇丂懍搙曄壔捈慄偺応崌
忋偺恾偼懍搙偑侽偐傜俇侽俲倣/帪娫傑偱捈慄慄揑偵曄壔偟偨応崌偱偁傞丅偙偺帪丄侾帪娫偱憱峴偟偨嫍棧偼偄偔傜偐丅偙傟偼愭傎偳偺峫偊曽偐傜憪怓偺柺愊偱偁傞偙偲偑暘偐傞丅恾俆偺侾帪娫偺挿曽宍偺柺愊偱偁傞俇侽俲倣偺敿暘偱偁傞偐傜俁侽俲倣偱偁傞偙偲偑暘偐傞丅偁傞偄偼嶰妏宍偺柺愊偺媮傔曽偱乮侾帪娫亊俇侽俲倣/帪娫乯/俀亖俁侽俲倣偲娙扨偵寁嶼偱偒傞丅偟偐偟捈慄偱側偔壓恾偺傛偆偵嬋慄偺応崌偼偳偆偩傠偆丅偦偆偼娙扨偵偼偄偐側偄丅
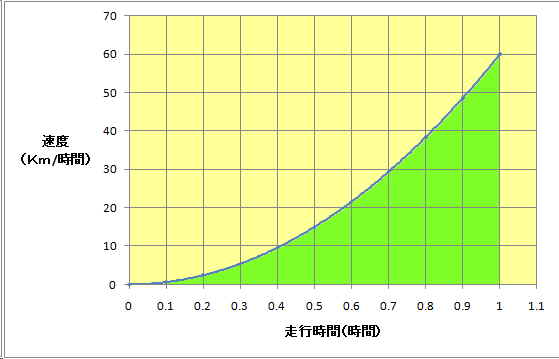
恾俈丂懍搙曄壔嬋慄偺応崌
恾俈偺応崌傕侾帪娫屻偺憱峴嫍棧偼憪怓偺柺愊偱偁傞偑丄尒偨栚偱偙偺柺愊偼寁嶼偱偒側偄丅偲偙傠偑偙偺惵怓偺慄偑愊暘壜擻側悢幃偱偁傟偽寁嶼偱偒傞偺偱偁傞丅偙傟偼俀師嬋慄側偺偱丄偦傟傪愊暘偟偰侾帪娫傑偱偺憱峴嫍棧亖俀侽俲倣偺摎偊偑摼傜傟傞丅偦傟偼偳偺傛偆偵悢幃傪愊暘偟偰寁嶼偱偒傞偐偼彮偟擄偟偔側傞偺偱偙偙偱偼棯偡傞乮師崁偺愊暘偺婎慴寁嶼傪嶲徠乯丅
嘦丂旝暘丒愊暘偺婎慴寁嶼
侾丂旝暘偺婎慴寁嶼
慜崁偺恾侾偱丄嫍棧傪倷乮俲倣乯偲偟帪娫傪倶乮帪娫乯偲偡傞偲丄帪懍俇侽俲倣偺帪偼倷亖俇侽倶側傞娭學幃偑摼傜傟傞丅偙偺偲偒丄帪娫偑宱偰偽偦傟偵墳偠偰嫍棧偑曄傢傞偺偱丄帪娫倶傪曄悢偲尵偄丄嫍棧倷偼倶偺娭悢偲傛傇丅偦偺娭悢傪堦斒偵倖乮倶乯傗倗乮倶乯側偳偺宍偱昞偡丅愭偺椺偱偼倖乮倶乯亖60倶偲偄偆娭悢傪掕媊偱偒傞丅
師偵堦斒揑側倖乮倶乯偵偮偄偰旝暘偡傞偙偲傪峫偊傞丅偙偺応崌慜崁偺恾俁偲摨偠峫偊曽偱媮傔傞丅丂倶亖a 偵偍偗傞倖乮倶乯偺旝暘傪師恾俉偱峫偊傞丅
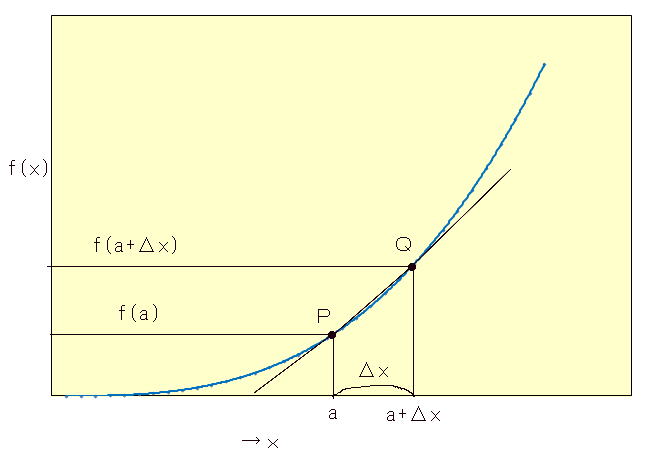
恾俉丂娭悢丂倖乮倶乯丂偺旝暘
恾俉偱惵怓偺嬋慄偼倖乮倶乯傪昞偟偰偄傞丅 丂倶亖a 偵偍偗傞旝暘偼丄嬋慄忋偺揰俹偱偺愙慄傪媮傔傞偙偲偵側傞丅丂偄偒側傝愙慄傪媮傔傜傟側偄偺偱傑偢倶亖a丂偐傜彮偟儮倶偩偗棧傟偨倶亖a+儮倶偵偍偗傞俻揰偲倶亖a偱偺俹揰傪寢傇捈慄偺岡攝傪媮傔傞丅丂椉揰偺崅偝偼f(x)偺倶偺偲偙傠偵丄偦傟偧傟a丄a+儮x傪戙擖偡傟偽椙偄丅廬偭偰俹揰
偺崅偝偼倖乮a)偱偁傝丄俻揰偺崅偝偼倖乮a亄儮x乯偲側傞丅丂偙偺偲偒俹偲俻傪寢傇捈慄偺岡攝偼丄
丂丂
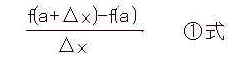 丂丂丂丂丂丂丂丂丂丂丂丂
丂丂丂丂丂丂丂丂丂丂丂丂
丂偲側傞丅偦偟偰偙偺儮倶傪偳傫偳傫尷傝側偔彫偝偔偡傞偙偲偵傛傝俻揰傪尷傝側偔俹揰偵嬤偯偗傟偽俹揰偱偺愙慄偵側傞丅偙傟傪悢妛揑側幃偱昞偡偲丄
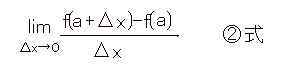
嘆幃偺慜偵彂偐傟偰偄傞婰崋偼儕儈僢僩儮倶僥儞僪侽偲撉傒丄嘆幃偵偍偄偰儮倶傪尷傝側偔僛儘偲偟偨帪偺嬌尷抣傪媮傔傞傕偺偱偁傞丅
嬶懱椺偲偟偰恾俉偺嬋慄偱傕偁傞丄倖乮倶乯亖倶2偺応崌傪峫偊偰傒傛偆丅
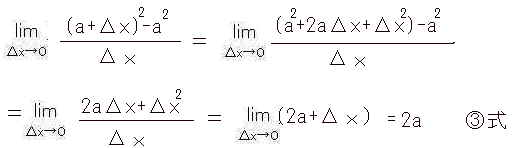
偙偺寢壥倶亖a 偵偍偄偰倖乮倶乯亖倶2丂傪旝暘偟偨抣偼俀a偲側傞丅丂偮傑傝倶亖a丂偵偍偗傞俹揰偱偺愙慄偱偁傞丅偙傟偑恾俁偺傛偆偵墶幉偑帪娫偱丄廲幉偑嫍棧側傜帪娫側傜帪娫a偵偍偗傞弖娫懍搙傪堄枴偡傞偙偲偵側傞丅丂側偍偙偺幃偱弶傔偐傜儮倶亖0偲偡傞偺偼暘曣偑侽偵側傝惉棫偟側偄丅丂儮倶偑僛儘偱偼側偔尷傝側偔僛儘偵嬤偄偲偄偆偙偲偱丄暘曣暘巕傪儮倶偱栺暘偱偒偨偺偱偁傞丅丂尷傝側偔偲偄偆尵梩偼側偵偐偁偄傑偄側姶偠偑偡傞偐傕偟傟側偄偑悢妛揑偵偼尩枾偵掕媊偝傟偰偄傞丅偦偺愢柧偼傓偮偐偟偔側傞偺偱偙偙偱偼棯偡傞偑丄奣擮揑偵儮倶偑偑僛儘偵嬤偯偗偽嘊幃偱俀a偵廂懇偡傞偙偲傪棟夝偟偰偄偨偩偗傟偽椙偄丅
偙偺旝暘傪昞偡幃偲偟偰

偲婰弎偝傟傞丅 偙傟傜傪倶亖a偵偍偗傞倖乮倃乯偺旝暘學悢偲屇傇丅丂偙偺旝暘學悢偼倃亖a 偩偗偱側偔偁傜備傞倃偺斖埻偱惉傝棫偮帪丄堦斒揑側幃偲偟偰

偱昞偣傞丅丂偙傟傪倖乮倶乯偺摫娭悢偲屇傇丅丂倖乮倶乯偑愭偺椺偺倖乮倶乯亖倶2偺応崌丄倖乫乮a)=2a偱偁偭偨偑丄傎偐偺擟堄偺揰倐偱傕倖乫乮b)=2b偑惉傝棫偮偺偱丄
堦斒揑偵倖乫乮倶乯亖俀倶側傞摫娭悢偱昞偡偙偲偑偱偒傞丅偙偺傛偆偵丄娭悢偑嬶懱揑偵暘偐偭偰偄傞応崌偼丄乮倶2乯乫亖俀倶偲偄偆彂偒曽傕偡傞丅
摫娭悢偑暘偐傟偽倶偑擟堄偺抣偱偺旝暘學悢偑暘偐傞丅丂椺偊偽倖乮倶乯亖倶2丂偵偮偄偰偄偊偽丄倶亖俈偱偺旝暘學悢偼倖乫乮俈乯亖俀亊俈亖侾係偲側傞丅
偦偺懠偺娙扨側摫娭悢偺岞幃偼師偺捠傝乮徹柧棯乯丄
丂丂乮a)'=0 (a偼悢抣乯丄乮倶乯乫亖侾丂丄乮倶俀乯乫亖俀倶丄乮倶俁乯乫亖俁倶俀丄丒丒丒丒丒丄乮倶値乯乫亖値倶乮値-侾乯丂丂乮値偼侾丏俀丏俁丏丒丒丒偺帺慠悢乯
丂丂(sin x)'=cos x丄(cosx)'=-sin x丂丂丂側偳
傑偨娭悢偺榓偺旝暘偵偮偄偰丄師偺岞幃偑惉傝棫偮乮徹柧棯乯丄
丂丂乷 a亊倖乮倶乯丂亄丂b亊倗(x)丂乸乫亖 a亊倖乫乮倶乯丂亄丂b亊倗乫(x)丂丂乮a,
b丂偼倶傪娷傑側偄悢抣乯
埲忋偺娭學傪巊偭偰丄椺偊偽乮俀倶3-俆倶2亄侾侽x-俉乯傪旝暘偡傞偲
乮俀倶3-俆倶2亄侾侽x-俉乯乫亖俀亊乮倶3乯乫乕俆亊乮倶2乯乫亄10乮倶乯乫-乮俉乯乫
丂丂丂丂丂丂丂丂丂丂丂丂丂丂 亖俀亊俁倶2乕俆亊俀倶亄侾侽亊侾乕侽亖俇倶2乕10倶亄10
偲側傞丅
俀丂愊暘偺婎慴寁嶼
(1)晄掕愊暘
丂嘥崁偱偼愊暘偺奣擮偲偟偰僌儔僼忋偱偺嬋慄乮傑偨偼捈慄乯偱埻傑傟偨柺愊傪昞偡偲愢柧偟偰偒偨偑丄偦偺偙偲偼屻弎偺掕愊暘偱愢柧偲偡傞偲偟偰丄傑偢愊暘偺掕媊傪愢柧偡傞丅愊暘偼旝暘偺媡墘嶼偱偁傝丄師偺娭學偵偁傞丅
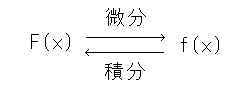
俥乮倶乯傪旝暘偟偰倖乮倶乯偵側傞偲偄偆娭學偼丂俥乫乮x)亖倖乮倶乯偱昞偟偨偑丄媡偵倖乮倶乯傪愊暘偟偰俥倶乯偵側傞偲偄偆娭學偼丄
![]()
偲婰弎偝傟傞丅丂偙偙偱佺偼僀儞僥僌儔儖偲撉傒愊暘偺墘嶼偺婰崋偱偁傞丅丂
偨偩栤戣偼旝暘偟偰倖乮倃乯偲側傞偺偼俥乮倶乯偵尷傜傟偢丄俥乮倶乯亄俁傕丄俥乮倶乯-俀傕旝暘偡傞偲倖乮倶乯偵側傞丅堦斒偵俥乮倶)亄俠乮俠偼擟堄偺掕悢乯傪旝暘偡傞偲倖乮倶乯偵側傞丅
偮傑傝丄丂乷俥乮倶乯亄俠乸乫亖俥乫乮倶乯亄乮俠乯乫亖俥乫乮倶乯亖倖乮倶乯偲側傞偐傜偱偁傞乮拲丗愭偺旝暘偺岞幃偵偁傞傛偆偵掕悢俠偼旝暘偡傞偲僛儘偲側傞乯
廬偭偰愭偺倖乮倶乯偺愊暘偺寢壥偼堦媊揑偵俥乮倶乯偱側偔丄堦斒幃偲偟偰師偺傛偆偵側傞丅
![]()
偙偙偱俥乮倶乯傪尨巒娭悢偲尵偄丄俠傪愊暘掕悢偲屇傇丅偦偟偰俠偼摿掕偺抣偵掕傑傜側偄偺偱偙偺愊暘傪晄掕愊暘偲尵偆丅
師偵偳偺傛偆偵偟偰愊暘偡傞偺偐傪愢柧偡傞丅丂丂偙傟偼旝暘偺岞幃偐傜媡嶼偡傞偙偲偵側傞丅
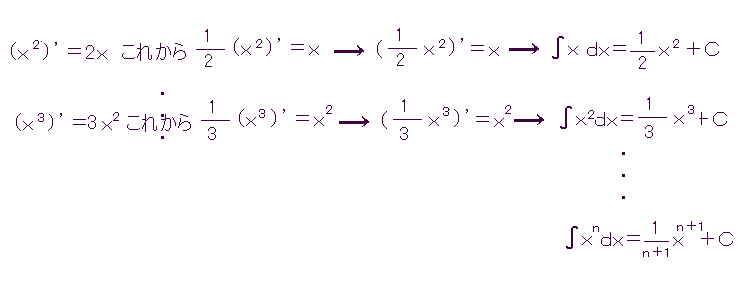 乮値偼侾丏俀丏俁丏丒丒丒偺帺慠悢乯
乮値偼侾丏俀丏俁丏丒丒丒偺帺慠悢乯
側偍娭悢偺榓偺愊暘傕旝暘偺帪偲摨條偵師偺幃偑惉傝棫偮乮徹柧棯乯丄
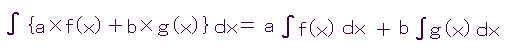
偙傟傜偵婎偯偒師偵寁嶼椺傪帵偡
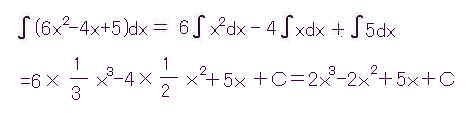
偲側傞丅丂偪側傒偵丄偙偺寢壥傪旝暘偡傞偲丄乮俀倶3亅俀倶2亄俆倶亄俠乯乫亖俇倶2亅係倶亄俆丂丂偲側傝丄愊暘偝傟傞慜偺尨巒娭悢偵栠傞偙偲偑妋擣偱偒傞丅
乮俀乯掕愊暘
晄掕愊暘偼慜崁偱愢柧偟偨傛偆偵丄俥乫乮倶乯亖倖乮倶乯側傜丄
![]()
偱偁傞丅偙偺娭學偵偁傞帪丄掕愊暘偱偼師偺傛偆偵掕媊偝傟傞丅丂
丂丂
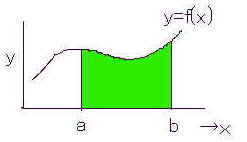
偙偺幃偺嵍曈偺撉傒曽偼僀儞僥僌儔儖a偐傜倐丒僄僼僄僢僋僗丒僨傿乕僄僢僋僗側偳偲尵偆丅丂偙傟偼倶亖a偐傜倶亖倐傑偱偺斖埻傪愊暘偡傞偙偲傪堄枴偡傞丅偦偟偰偦傟偼忋偺恾偵帵偡傛偆偵a,b娫偺斖埻偱埻傑傟偨椢怓晹暘偺柺愊偲側傞丅丂側偤偦偺傛偆偵側傞偐偼師偵愢柧偡傞丅側偍晄掕愊暘偺傛偆偵晄掕偺俠傪娷傑偢抣偑堦媊揑偵寛傑傞偺偱掕愊暘偲屇傫偱偄傞丅丂
壓恾丂倷亖倖乮倶乯偺僌儔僼偵偍偄偰倶亖倶0偲倶亖倶偱埻傑傟傞柺愊傪俽乮倶乯偲偡傞丅丂偦偟偰倶0丂埲崀偵x=a 偲x=b丂偑偁傞偲偡傞丅丂偮傑傝倶0亙a亙x亙倐 偵埵抲晅偗偟偰峫偊傞丅
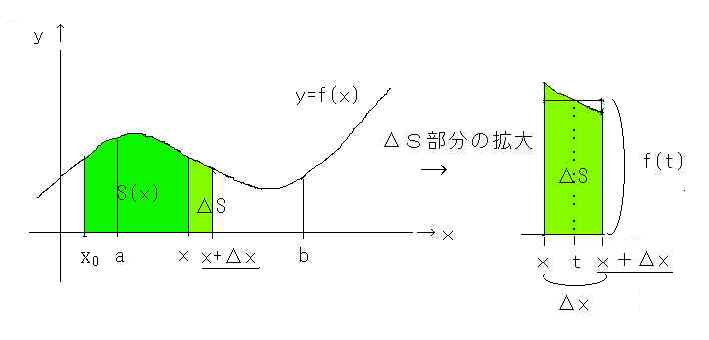
恾俋丂掕愊暘偺愢柧恾丂侾
倶傛傝儮倶偼側傟偨強偱偺柺愊偺憹暘傪儮俽偲偡傞丅丂偙偺儮俽偼奼戝恾偵偍偗傞崅偝倖乮倲乯偺挿曽宍偲柺愊偑堦抳偡傞倶亖倲偺抧揰偑懚嵼偡傞敜偱偁傞丅
偮傑傝儮俽亖儮倶亊倖乮倲乯丂偲側傞丅丂丂丂偟偐偟儮倶仺侽丂偺偲偒丂倲仺倶丂偲側傝丂倖乮倲乯仺倖乮倶乯丂偲側傞偙偲偐傜師幃偑惉傝棫偮丅
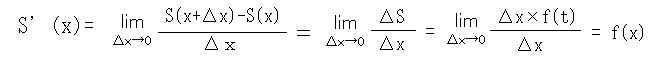
偮傑傝俽乫乮倶乯亖倖乮倃乯偲偄偆娭學偵偁傞偙偲偐傜丄師偺晄掕愊暘偑惉傝棫偮丅
![]()
偙偺娭學偑惉傝棫偮帪丄a偐傜b偺掕愊暘偼掕媊偐傜丄
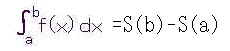
偲側傞丅偙傟偼側偵偐偲偄偆偲丄愭偺僌儔僼偵偍偄偰丄倶亖a丂偲丂倶亖b 偺娫偱倖乮倶乯偲倶幉偱埻傑傟偨柺愊偱偁傞乮壓恾偺烌怓偺晹暘乯丅偙偺偙偲偐傜掕愊暘偼f(x)偺僌儔僼偵偍偄偰倶偺偁傞嬫娫撪偱偺柺愊偱偁傞偲尵偊傞丅
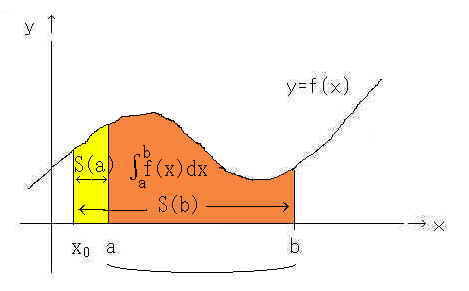
恾10丂掕愊暘偺愢柧恾丂俀
師偵慜崁偺恾俉乮壓恾乯傪椺偵庢偭偰寁嶼傪帋傒傞丅丂偙偺僌儔僼偼丄憱峴帪娫乮倶乯偲懍搙乮倷乯偲偺娭學偱偁傞丅丂偙偺偲偒丄倷亖倖乮倶乯亖60倶2偺娭學幃偱偁傞丅

憪怓偺柺愊偑憱峴嫍棧偲側傞丅丂僗僞乕僩偟偰侾帪娫屻偺憱峴嫍棧偼丂
丂丂
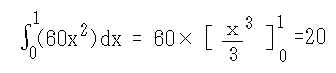
偲側傝侾帪娫偱俀侽俲倣憱峴偟偨偙偲偑暘偐傞丅丂偪側傒偵搑拞偺侽丏係帪娫偐傜侽丏俇帪娫傑偱偺憱峴嫍棧偼丄
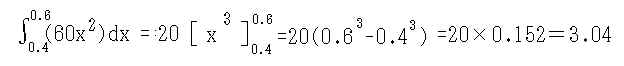
偲偄偆寁嶼偵側傝丄偙偺娫栺俁俲倣憱峴偟偨偙偲偑暘偐傞丅
埲忋