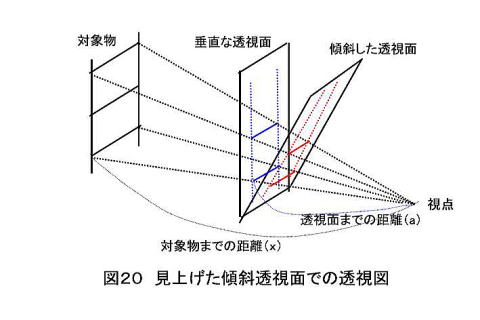

上の図は透視面をこれまでの一点、二点透視図の時と同様垂直に立てた時と、傾斜した面で
仰ぎ見た時の比較をしました。対象物は梯子のようなものが高く伸びたものを想定しています。
この場合図から分かる様に垂直な透視面では相似形の関係から対象物の幅と透視面での幅(青)
の比は変わりません。つまり高く伸びても幅(青)は変わらず一定です。
これに対して傾斜した透視面での幅(赤)は上に行くに従って垂直な透視面から遠ざかるので青の
幅に対して赤の幅はどんどん小さくならことが分ると思います。
つまり上に行くに従って幅が狭くなっていきます。 これが三点透視図の原理です。
次にこのときの消失点を考えるため分かり易く次図のように図20を真横から見てみます。
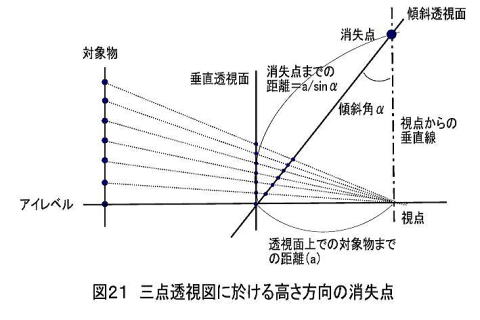
この図で等間隔の梯子状のバーは横から見て●で示しています。これが無限に高さ方向に続くとします。
このとき垂直透視面ではこの●は同じく等間隔で無限に続くのに対して、傾斜面ではこの間隔がだんだん
狭くなり、視点から真上の傾斜面との交点に収束し、それを超えて●は存在しません。
つまりここが消失点になります。この傾斜面上での消失点までの距離は図からa/sinαになります。
実際の高さとしてはaが対象物までの距離と考えれば良いのです。
例えば50m離れたところから45°の傾斜面でみると消失点までの距離は50m/sin45°=100mとなります。
もし対象物が20mの高さのビルなら、その5倍の高さに消失点があることになります。なおα=0°の場合は
垂直面になり、消失点までの距離はsin0°=0だから無限大となって消失点は存在しません(どこまでも平行)。
またαがマイナスの時は傾斜面が下向きの場合であり、消失点までの距離もマイナスとなり消失点は視点より
下の位置になります(図19参照)。